TREE
merupakan salah satu bentuk struktur data yg tidak linear dan menggambarkan hubungan yg bersifat hierarkis astara data satu dengan yg lain.
bisa disimpulkan bahwa tree merupakan kumpulan node dengan satu elemen khusus yg di sebut root.
 |
| contoh tree |
berikut adalah istilah umum yg ada pada tree:
- preodecessor: node yg berada diatas node tertentu.
- successor: node yg brada di bawah node tertentu.
- ancestor: semua node yg terletak sebelum node tertentu terletak pada jalur yg sama.
- descendant: seluruh node tertentu yg terletak di bawah node tertentu dan ada pada satu jalur.
- parent: predecessor di atas satu node.
- child: successor satu node dibawah suatu node.
- sibling: node2 yg memiliki satu parent yg sama dengan suatu node,
- Subtree : bagian dari tree yang berupa suatu node beserta descendantnya dan memiliki semua karakteristik dari tree tersebut.
- Size : banyaknya node dalam suatu tree.
- Height : banyaknya tingkatan/level dalam suatu tree.
- Root : satu-satunya node khusus dalam tree yang tak punya predecssor.
- Leaf : node-node dalam tree yang tak memiliki seccessor
- Degree : banyaknya child yang dimiliki suatu node
BINARY TREE
binarry tree adalah tree dengan maksimal 2 subnode di tiap nodenya.
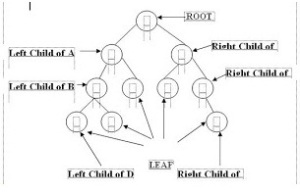
tipe2 binary tree:
- perfect: binary tree dengan setiap tingkatnya memiliki kedalaman yg sama.
- complete: binary tree yg dimana setiap tingkat, kecuali muhgkin yg terahir benar2 terisi.
- skewed: binary tree yg setiap nodenya paling banyak memiliki satu anak.
- balance: binary tree yg dimana tidakada leaf yg lebih jauh dari root daripada leaf lainnya.
operasi pada binary tree:
- create: membuat binary tree baru yg masih kosong.
- clear: mengosongkan binary tree yg sudah ada.
- empty: function untuk memeriksa apakah binary tree tersebut masih kosong atau tidak.
- insert: memasukkan node kedalam tree.
- find: mencari root, parent, left child atau right child dari suatu node,
- update: mengubah isi dari node yg di tunjuk oleh pointer.
- retrieve: mengetahui isi dari node yg ditunjuk oleh pointer.
- deletesub: menghapus sebuah subtree.
- characteristic: mengetahui carakteristic suatu tree.
- traverse: mengunjungi seluruh node-node pada tree, masing masing sekali.
EXPRESSION TREE
prefix: *+abc
postfix: ab+c*
infix: (a+b)*c
yinggal di ubah sesuai aturan binary tree / tree

Tidak ada komentar:
Posting Komentar